[Data Science] Linear Algebra

[금일의 개념정리]

• base
• unit vector
• span
• Linear Dependent
• Linear Independent
• Projection Vector
• Variance & Covariance
• Dot Product
• Correlation & Correlation Value
• Gaussian Elemination
• Rank
• 최종: 왜 이러한 개념들이 인공지능과 관련이 되어 있는지!

---

Base?

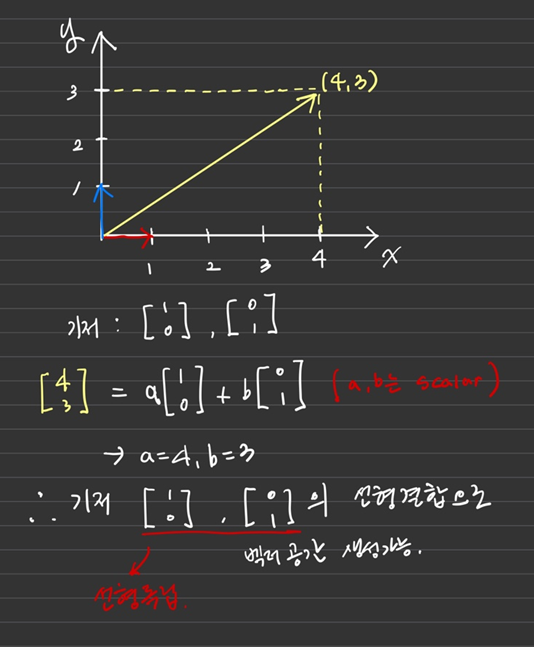
• 선형대수학에서 어떤 벡터 공간의 기저란 그 벡터 공간을 선형생성하는 선형 독립 벡터들의 집합이다.
• 벡터 공간의 임의의 벡터에게 선형결합으로서 유일한 표현을 부여하는 벡터이다.
• 아래의 그림에서 보여준 예시 기저만이 생성된 벡터 공간의 유일한 기저는 아니다. [x,0],[0,y]로 표현되는 모든 벡터가 특정 벡터 공간의 기저가 될 수 있다. 다만, 차원에 따라서 기저를 구성하는 벡터의 수는 유일하다. 아래 그림은 2차원을 표현했고 기저를 구성하는 벡터의 수는 2개이다.
• 선형 종속인 벡터는 기저 벡터가 될 수 없다.

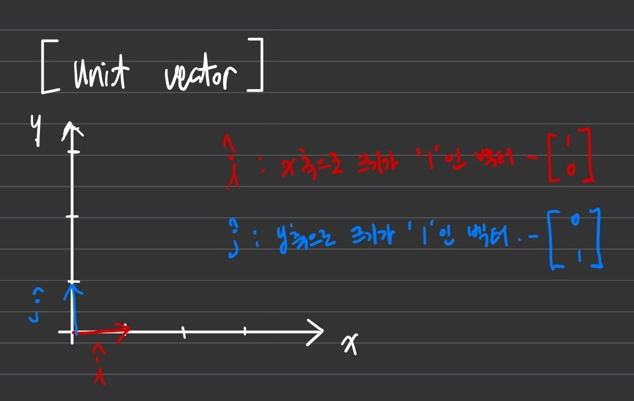
Unit Vector?

• 표준 기적 벡터라고 할 수 있다.

span?

• 주어진 두 벡터의 조합(합 or 차)으로 만들 수 있는 모든 벡터의 집합이다.(면 or 선)
• 면인 경우는 선형 독립인 두 벡터일 때, 선인 경우는 선형 종속인 두 벡터 조합의 집합이다.

Linear Dependent & Linear Independent?

1. Linear Dependent
   • 3차원 공간에서 세 번째 벡터가 두 벡터의 스팬에 놓여 있는 경우
   • 벡터를 추가해도 기존의 스팬이 더 이상 확장되지 않는 경우
   • 하나의 벡터를 제외시켜도 스팬의 범위가 축소되지 않는 경우
   • 벡터들 중 하나가 다른 두 벡터의 선형 조합으로 표현되는 경우
   • 2차원인 경우, 두 벡터의 선형조합의 스팬이 선인 경우
2. Linear Independent
   • 기존의 벡터에 새로운 벡터 추가시 기존 스팸의 범위가 더 확장되는 경우
   • 2차원일 때, 두 벡터의 선형조합의 스팬이 면인 경우

Projection Vector?

• 이 개념을 정리하기 전에 projection(사영) 이란 뭘까?
  • 어떤 도형에 빛을 비춘다면 그 그림자가 바로 일종의 ‘사영’이 된다.
• 아래 그림을 보면, projection vector를 구하는 법이 나와 있다. 그렇다면 projection vector를 사용하는 이유는 무엇인가?
  • 데이터를 표기하기 위해서는 x,y라는 두 개의 feature가 필요하다. 하지만 어느 때에는 하나의 feature만 필요한 경우가 있을 것이다. 이런 경우를 위해 projection vector를 사용한다.
    • 하나의 feature만 필요한 경우가 언제일까?

Variance & Covariance?

1. Variance
   • 데이터가 퍼져 있는 정도를 나타내는 지표이다.
2. Covariance
   • 1개의 변수의 값이 변화할 때 다른 변수가 어떠한 연관성을 나타내며 변하는지를 측정하는 것이다.

Dot Product?

• 내적의 의의 \(a \cdot b = |a||b|\cos(\theta)\) \(\cos(\theta) = \frac{a \cdot b}{|a||b|}\)
  1. 두 벡터사이의 내적은 스칼라로 나온다. 그래서 내적값과 벡터의 크기를 안다면 사이각을 구할 수 있다.
     • 위의 식에서 볼 수 있듯이 두 벡터가 서로 수직이기 위한 필요충분조건은 아래와 같다. \(a \cdot b = 0\)
  2. 사영이라는 개념에 많이 사용된다.

Correlation & Correlation coefficient

1. Correlation
   • 상관 관계 or 상관 or 상관 분석은 어떤 두 변수간에 선형 or 비선형관계인지를 분석하는 방법이다.
2. Correlation Coefficient
   • 두 변수간에 독립적인 관계 일수도 상관 관계일수도 있는데 이러한 두 변수간의 관계의 정도를 나타내는 것을 상관 계수라고 한다. - 상관 계수는 두 변수간의 상관 정도를 나타낼 뿐 두 변수간의 인과 관계를 설명하는 것은 아니다.

Rank

• 행렬의 열의 벡터들 중 선형 독립인 벡터들의 개수를 말한다.
• 행렬의 차원과는 다른 의미인데, 그 이유는 행렬의 열, 행 벡터중에 서로 선형 종속 관계에 있는 것이 있을 수 있기 때문이다.

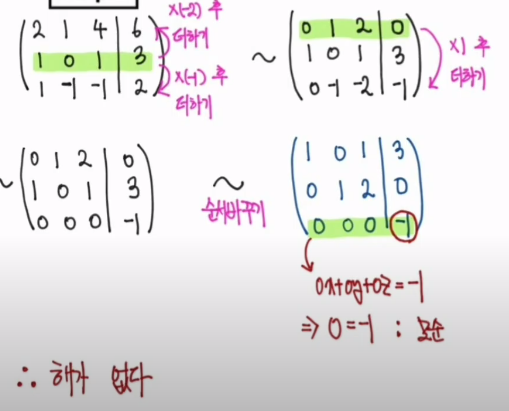
Gaussian Elemination

• Rank를 확인하는 방법 중의 하나
• 연립 일차방정식의 해를 구할 때 사용하는 방법인데, 행렬에 가우스 소거법을 사용해서 남게 되는 행의 개수가 행렬의 rank가 된다.