[Data Science] Basic Derivative

개요

• 최적화와 미분의 관계에 대해 알아봅니다.
• 미분, 편미분, Chain Rule의 차이를 이해하고 계산을 할 수 있게 됩니다.
• 도함수를 파이썬으로 직접 구현하거나 scipy 라이브러리를 활용해서 구할 수 있습니다.

1. 미분

1-1. 미분이란?

미분은 데이터 사이언스를 공부한다면 피할 수 없는 숙명과도 같은 존재이다. 미분뿐만이 아니라 수학 자체를 피할 수 없다.

미분이란 단어는 작을 미(微)와 나눌 분(分). 즉 "작게 나눈다"라는 의미입니다. 무엇을 작게 나누는 것일까요? 바로 함수입니다.

함수를 작게 나눈다는 것의 의미는 무엇일까?

입력 값 x를 아주 미세하게 변화 시킨 후에 입력했을 때 그 결과값이 어떻게 바뀌는지를 보는 것이라고 생각하면 됩니다.

아래의 그림처럼 x의 변화량을 0에 가깝게 했을 때의 결과를 확인함으로써 입력과 결과에 관계에 대해 알 수 있다. 즉, 미분은 특정한 파라미터(input, x)에 대해서 나오는 결과값(output, y)이 변화하는 정도를 계산하는 것입니다.

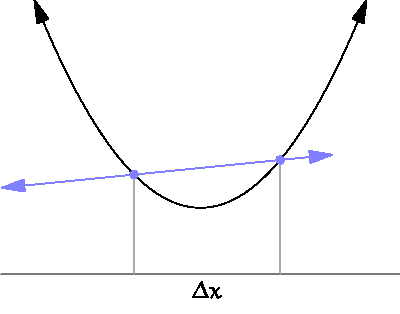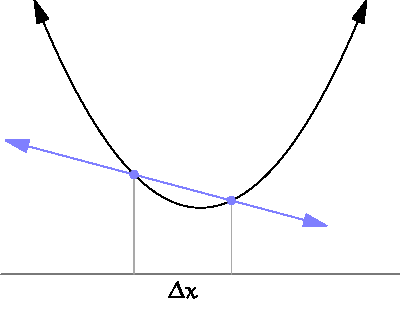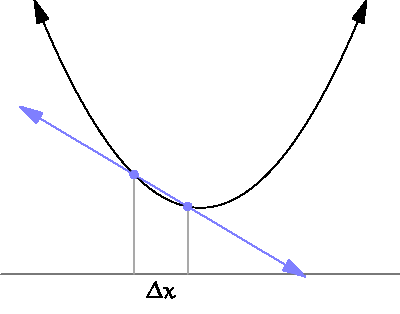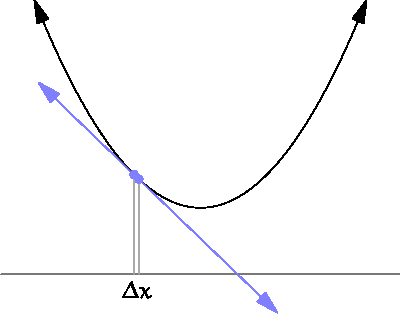
기울기는 도함수의 개념을 쉽게 말한 것이다.

미분과 데이터 사이언스는 무슨 관계?

오차함수는 왜 도함수 = 0 과 무슨 관계가 있지..?

1-2. 미분 공식

$f’(x) = 상수 -> f’(x) = 0$

# 예시 1 : Numerical Method

# f(x) = 5
def f(x):
    return 5

def numerical_derivative(fx, x):
    delta_x = 1e-5

    return (fx(x + delta_x) - fx(x)) / delta_x

print(numerical_derivative(f, 1)) #output: 0.0

# 예시 2 : Scipy의 derivative 활용
from scipy.misc import derivative

# 두 방법의 결과값 비교
derivative(f,1, dx=1e-6) == numerical_derivative(f, 1)
#output: True

$f(x) = ax^n –> f’(x) = anx^(n-1)$

해당 미분법은 일명 Power Rule이라고 불리운다.

# 같은 결과를 numerical method를 활용해서 계산해보겠습니다
def f(x):
    return 3*(x**4) + 10

def numerical_derivative(fx, x):
    delta_x = 1e-5

    return (fx(x + delta_x) - fx(x)) / delta_x

print(numerical_derivative(f, 2)) #output: 96.0007200028201

# 예시 2 : Scipy의 derivative 활용
from scipy.misc import derivative

# 두 방법의 결과값 비교
print(derivative(f,2, dx=1e-5)) #output: 96.0000000031158

derivative(f,2, dx=1e-5) == numerical_derivative(f, 2)  #output: False
#delta X의 값은 같지만 Rounding 에러로 인해 두 결과가 미묘하게 다른 것을 확인하실 수 있습니다.

$f(x) = e^x –> f’(x) = e^x$

$f(x) = lnx –> f’(x) = 1/x$

1-3. 편미분

상당히 많은 머신러닝의 오차함수는 여러 파라미터로 이뤄져 있다. 이러한 오차함수를 미분할 때 사용하는 것이 편미분이다.

예제) $f(x,y) = x^2 + 4xy + 9y^2$라는 함수의 $f’(1, 2)$의 값을 계산해보겠습니다.

이를 위해서 해야 하는 것은 다음과 같습니다 :

$x$에 대해 편미분 $\partial f(x,y) \over \partial x$ = $2x + 4y$

${f’(1, 2) \over \partial x}$ = $2 \cdot (1) + 4 \cdot (2) = 10$

$y$에 대해 편미분 $\partial f(x,y) \over \partial y$ = $4x + 18y$

${f’(1, 2) \over \partial y}$ = $4 \cdot 1 + 18 \cdot 2 = 40$

1-4. chain rule

함수의 함수를 미분하기 위해 사용하는 방식이다. 이를 합성함수라고 부르기도 하며 공식은 다음과 같다.

공식

$F(x) = f(g(x))$

$F’(x)$ $\rightarrow$ $f’((g(x)) \cdot g’(x)$

Deep Learning의 Back Propagation에서 chain rule이 많이 사용된다. Back Propagation에 대해서는 시간이 될 때 한 번 찾아보기로 하자.